- Автор admin carl@lifeloveeveryday.com.
- Public 2023-12-16 19:27.
- Последнее изменение 2025-01-23 15:34.

Примеры золотого сечения можно найти повсюду в классической архитектуре, произведениях искусства, природе и даже музыке. Это выражение пропорции, также известное как Божественное соотношение, обеспечивает гармоничную композицию за счет применения иррационального числа (1,618) в дизайне, как естественном, так и созданном руками человека. Скорее всего, вы не знаете о математике, лежащей в основе красоты Золотого сечения, потому что оно создает объекты и музыку, которые естественным образом находят вас приятными, не нуждаясь в каких-либо объяснениях.
Золотое сечение в архитектуре
Золотое сечение создает почти идеальную красоту в природе и искусстве. Когда вы начнете искать примеры золотого сечения в повседневной жизни, вы можете быть удивлены множеством случаев, когда оно использовалось для создания множества монументальных зданий и сооружений. Когда в архитектуре используется золотое сечение, говорят, что здание создано с использованием «сакральной архитектуры». Применяя расчет золотого сечения к квадрату, архитекторы и дизайнеры могут создать золотой прямоугольник, который, как полагают, имеет наиболее эстетически приятные пропорции для человеческого глаза.
Пример золотого прямоугольника: Парфенон

Фидий, греческий скульптор, использовал золотое сечение в своей работе, особенно когда он начал работать с полосами, которые он ваял прямо над колоннами Парфенона. Также важно отметить, что числовое значение, присвоенное золотому сечению Фи, было названо в его честь.
Если вы измерите внешние размеры Парфенона, вы обнаружите, что он не только образует золотой прямоугольник, но и между колоннами имеется множество золотых прямоугольников. Это священное сооружение является прекрасным примером золотого сечения в архитектуре.
Пример Золотого треугольника: Великая пирамида в Гизе
Золотое сечение, золотой прямоугольник и золотой треугольник - все это можно найти в совершенстве одного из семи чудес света - Великой пирамиды Гизы. Чтобы найти золотое сечение, вам нужно разделить квадрат основания пирамиды пополам и провести вертикальную линию вверх по центру пирамиды. Когда он соединяется с наклонной стороной пирамиды, вы можете легко увидеть, как он образует Золотой Треугольник с соотношением 1,618, Золотое Сечение.
Другие архитектурные примеры
Вы можете найти множество примеров древней и современной сакральной архитектуры и зданий золотого сечения.
- Шартрский собор - Центр, Франция
- Нотр-Дам - Париж, Франция
- Девичий притвор - Акрополь, Афины
- Тадж-Махал - Агра, Индия
- Здание Организации Объединенных Наций - Нью-Йорк, Нью-Йорк
Золотое сечение в примерах искусства
Вы можете найти множество примеров мастеров-художников, которые использовали золотое сечение. Эти совершенные произведения были созданы с использованием соотношения золотых прямоугольников и золотых треугольников. Искусство, созданное на основе Золотого прямоугольника, оказывается более приятным для человеческого глаза. Это одна из загадок, окружающих идеальный прямоугольник и золотое сечение.
Золотое сечение в искусстве

Примеры искусства золотого сечения:
- Леонардо Ди Винчи - Мона Лиза, Витрувианский человек
- Боттичелли - Рождение Венеры
- Микеланджело - Святое Семейство, 'Давид'
- Рафаэль - Распятие
- Рембрандт - Автопортрет
- Сальвадор Дали - Таинство Тайной Вечери, Постоянство памяти
Использование золотого сечения в художественной композиции
Внутри золотого прямоугольника есть определенные области, которые кажутся более привлекательными визуально, чем другие области. Эти точки обнаруживаются путем рисования линии от нижнего угла прямоугольника до противоположного угла и повторения ее с другим нижним углом. Эти линии будут пересекаться точно в центре золотого прямоугольника. Затем измерьте середину каждой линии, начиная с центральной точки. Эти четыре точки называются глазами прямоугольника (золотое сечение). Затем основной фокус картины рисуется или раскрашивается в пределах этих точек интереса (соотношений).
Золотое сечение в музыке

Музыка состоит из числовых значений, и когда для создания музыкального произведения используется золотое сечение, оно становится живым примером математики. Последовательность Фибоначчи также распространена в музыке:
- В гамме восемь нот.
- Третья и пятая ноты составляют основу аккордов.
- Длина или октава любой ноты составляет 13 нот.
Последовательность продолжается на протяжении всего музыкального произведения и становится более сложной по мере достижения золотого сечения.
Композиторы, использовавшие золотое сечение
Некоторые из самых известных композиторов-классиков использовали Золотое сечение и последовательность Фибоначчи в своих музыкальных произведениях, в том числе Бах, Бетховен, Шопен и Моцарт. Некоторые современные композиторы, такие как Кейси Монговен, исследовали золотое сечение в своей музыке.
Примеры золотого сечения в природе

Где в природе встречается золотое сечение? Он находится в золотой спирали или спирали Фибоначчи, которую можно создать с помощью золотого сечения. Это явление широко распространено в мире природы. Листья растения растут так, чтобы как можно больше листьев могло подниматься по стеблю по спирали. Новый лист образуется только после того, как сформировался предыдущий.
- Спиральные кактусы
- Спиральные галактики
- Подсолнухи
Цветы с последовательностью Фибоначчи
У некоторых цветов лепестки соответствуют последовательности Фибоначчи:
- Три лепестка:Ирис, лилия, орхидеи, триллиум
- Пять лепестков: Лютики, герань, гибискус, ипомея, настурция
- Восемь лепестков: Дельфиниумы
- 13 лепестков: Некоторые сорта ромашки, амброзии, бархатцев
Спираль Фибоначчи в сосновых шишках

В зависимости от породы дерева вы также можете увидеть работу золотого сечения в ряду чисел Фибоначчи в сосновых шишках. Вы можете найти серию из восьми спиралей на одной стороне шишки и 13 спиралей на другой. Другой узор из сосновых шишек имеет пять спиралей с одной стороны и восемь с другой.
Золотое сечение у человека
Это соотношение также важно не только для того, как люди смотрят друг на друга, но и для того, как работают их тела, и для их ДНК.
ДНК раскрывает золотое сечение
Один из самых удивительных примеров золотого сечения находится в структуре ДНК человека. Это можно увидеть на одном поперечном сечении ДНК, на котором видно, что двойная спираль ДНК имеет форму десятиугольника. Это комбинация двух пятиугольников, повернутых друг к другу на 36 градусов, образует двойную спираль ДНК. Сама двойная спиральная спираль образует пятиугольник. Даже одна молекула ДНК раскрывает основу Золотого Сечения или Божественной Пропорции.
Математика золотого сечения
Найти золотое сечение в реальной жизни очень просто, оно проявляется повсюду вокруг вас. Это математический трюизм, который используется для определения того, что обычно называют идеальным числом, встречающимся в природе, которое веками дублировалось и имитировалось людьми. Упрощенная красота этого номера скрывает сложность его исполнения. Чтобы понять теорию золотого сечения, вы должны сначала изучить последовательность чисел Фибоначчи.
Последовательность Фибоначчи и золотое сечение
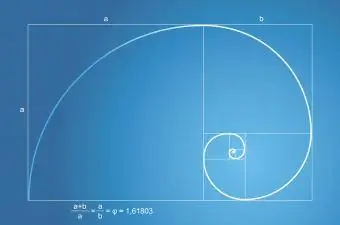
Последовательность или ряд Фибоначчи связана с золотым сечением. Ряд Фибоначчи проявляется в количестве листьев на растении и количестве лепестков на цветке. Спираль Фибоначчи, встречающаяся в природе, всегда является частью золотого прямоугольника с золотым сечением.
Расчет рядов Фибоначчи прост:
- Последовательность начинается с 0 и 1.
- Просто сложите два последних числа, чтобы получить следующее число в серии.
- 0+1=1, 1+1=2, 1+2=3, 2+3=5, 3+5=8 и так далее.
- Этот пример ряда Фибоначчи выглядит следующим образом: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и т. д.
Отношение Фибоначчи к золотому сечению реализуется, когда оно складывается вперед, дальше и дальше. Чем больше вы добавляете рядов, тем ближе вы приближаетесь к золотому сечению.
Создание золотого прямоугольника и треугольника
Чтобы создать золотой прямоугольник с помощью последовательности Фибоначчи, вы начинаете с квадрата. Вы начнете строить прямоугольник, добавляя к исходному квадрату еще один квадрат. Не забывайте использовать формулу: 0+1=1 - первый квадрат, 1+1=2 - вы добавите еще один квадрат.1+2=3 вы добавите три квадрата, а затем 2+3=5 вы добавите пять квадратов. Вы продолжите добавлять квадраты и в конечном итоге сформируете золотой прямоугольник.
Золотой треугольник можно создать, разделив золотой прямоугольник пополам от одного угла к противоположному углу. Это создает треугольник, в котором три его стороны или углы имеют пропорцию 2:2:1, то есть две длинные стороны равны по длине, а короткий угол равен ровно половине длины двух длинных.
Золотое сечение в реальном мире
Золотое сечение часто называют Божественным сечением из-за его важности в природе и в человеческих телах. Открытие того, что золотое сечение присутствует во многих живых существах, породило уважение к этой волшебной пропорции, и сегодня оно продолжает вдохновлять художников и творцов.






